Stuart
Staniford 1
Vern Paxson 2
Nicholas
Weaver 3
Silicon Defense
ICSI Center for Internet Research
UC Berkeley
[email protected]
[email protected]
[email protected]
To
Appear in the Proceedings of the 11th USENIX Security Symposium
(Security '02)
The ability of attackers to rapidly gain control of vast numbers of Internet hosts poses an immense risk to the overall security of the Internet. Once subverted, these hosts can not only be used to launch massive denial of service floods, but also to steal or corrupt great quantities of sensitive information, and confuse and disrupt use of the network in more subtle ways.
We present an analysis of the magnitude of the threat. We begin with a mathematical model derived from empirical data of the spread of Code Red I in July, 2001. We discuss techniques subsequently employed for achieving greater virulence by Code Red II and Nimda. In this context, we develop and evaluate several new, highly virulent possible techniques: hit-list scanning (which creates a Warhol worm), permutation scanning (which enables self-coordinating scanning), and use of Internet-sized hit-lists (which creates a flash worm).
We then turn to the to the threat of surreptitious worms that spread more slowly but in a much harder to detect "contagion" fashion. We demonstrate that such a worm today could arguably subvert upwards of 10,000,000 Internet hosts. We also consider robust mechanisms by which attackers can control and update deployed worms.
In conclusion, we argue for the pressing need to develop a "Center for Disease Control" analog for virus- and worm-based threats to national cybersecurity, and sketch some of the components that would go into such a Center.
If you can control a million hosts on the Internet, you can do enormous damage. First, you can launch distributed denial of service (DDOS) attacks so immensely diffuse that mitigating them is well beyond the state-of-the-art for DDOS traceback and protection technologies. Such attacks could readily bring down e-commerce sites, news outlets, command and coordination infrastructure, specific routers, or the root name servers.
Second, you can access any sensitive information present on any of those million machines--passwords, credit card numbers, address books, archived email, patterns of user activity, illicit content--even blindly searching for a "needle in a haystack," i.e., information that might be on a computer somewhere in the Internet, for which you trawl using a set of content keywords.
Third, not only can you access this information, but you can sow confusion and disruption by corrupting the information, or sending out false or confidential information directly from a user's desktop.
In short, if you could control a million Internet hosts, the potential damage is truly immense: on a scale where such an attack could play a significant role in warfare between nations or in the service of terrorism.
Unfortunately it is reasonable for an attacker to gain control of a million Internet hosts, or perhaps even ten million. The highway to such control lies in the exploitation of worms: programs that self-propagate across the Internet by exploiting security flaws in widely-used services.4 Internet-scale worms are not a new phenomenon [Sp89,ER89], but the severity of their threat has rapidly grown with (i) the increasing degree to which the Internet has become part of a nation's critical infrastructure, and (ii) the recent, widely publicized introduction of very large, very rapidly spreading Internet worms, such that this technique is likely to be particularly current in the minds of attackers.
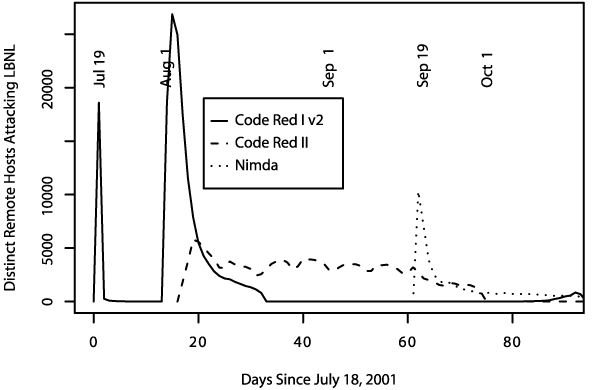
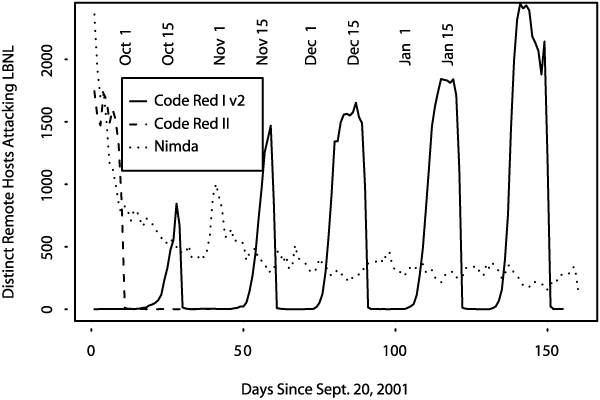
We present an analysis of the magnitude of the threat. We begin with a mathematical model derived from empirical data of the spread of Code Red I v2 in July and August, 2001 (Section 2). We then discuss techniques employed for achieving greater effectiveness and virulence by the subsequent Code Red II and Nimda worms (Section 3). Figures 1 and 2 show the onset and progress of the Code Red and Nimda worms as seen "in the wild."
In this context, we develop the threat of three new techniques for highly virulent worms: hit-list scanning, permutation scanning, and Internet scale hit-lists (Section 4). Hit-list scanning is a technique for accelerating the initial spread of a worm. Permutation scanning is a mechanism for distributed coordination of a worm. Combining these two techniques creates the possibility of a Warhol worm,5seemingly capable of infecting most or all vulnerable targets in a few minutes to perhaps an hour. An extension of the hit-list technique creates a flash worm, which appears capable of infecting the vulnerable population in 10s of seconds: so fast that no human-mediated counter-response is possible.
We then turn in Section 5 to the threat of a new class of surreptitious worms. These spread more slowly, but in a much harder to detect "contagion" fashion, masquerading as normal traffic. We demonstrate that such a worm today could arguably subvert upwards of 10,000,000 Internet hosts.
Then in Section 6, we discuss some possibilities by which an attacker could control the worm using cryptographically-secured updates, enabling it to remain a threat for a considerable period of time. Even when most traces of the worm have been removed from the network, such an "updatable" worm still remains a significant threat.
Having demonstrated the very serious nature of the threat, we then in Section 7 discuss an ambitious but we believe highly necessary strategy for addressing it: the establishment at a national or international level of a "Center for Disease Control" analog for virus- and worm-based threats to cybersecurity. We discuss the roles we envision such a Center serving, and offer thoughts on the sort of resources and structure the Center would require in order to do so. Our aim is not to comprehensively examine each role, but to spur further discussion of the issues within the community.
The first version of the Code Red worm was initially seen in the wild on July 13th, 2001, according to Ryan Permeh and Marc Maiffret of Eeye Digital Security [EDS01a,EDS01b], who disassembled the worm code and analyzed its behavior. The worm spread by compromising Microsoft IIS web servers using the .ida vulnerability discovered also by Eeye and published June 18th [EDS01c] and was assigned CVE number CVE-2001-0500 [CV01].
Once it infected a host, Code-Red spread by launching 99 threads which generated random IP addresses, and then tried to compromise those IP addresses using the same vulnerability. A hundredth thread defaced the web server in some cases.
However, the first version of the worm analyzed by Eeye, which came to be known as CRv1, had an apparent bug. The random number generator was initialized with a fixed seed, so that all copies of the worm in a particular thread, on all hosts, generated and attempted to compromise exactly the same sequence of IP addresses. (The thread identifier is part of the seeding, so the worm had a hundred different sequences that it explores through the space of IP addresses, but it only explored those hundred.) Thus CRv1 had a linear spread and never compromised many machines.
On July 19th, 2001, a second version of the worm began to spread. This was suspected informally via mailing list discussion, then confirmed by the mathematical analysis we present below, and finally definitively confirmed by disassembly of the new worm. This version came to be known as CRv2, or Code Red I.
Code Red I v2 was the same codebase as CRv1 in almost all respects--the only differences were fixing the bug with the random number generation, an end to web site defacements, and a DDOS payload targeting the IP address of http://www.whitehouse.gov/.
We developed a tentative quantitative theory of what happened with the spread of Code Red I worm. The new version spread very rapidly until almost all vulnerable IIS servers on the Internet were compromised. It stopped trying to spread at midnight UTC due to an internal constraint in the worm that caused it to turn itself off. It then reactivated on August 1st, though for a while its spread was suppressed by competition with Code Red II (see below). However, Code Red II died by design [SA01] on October 1, while Code Red I has continued to make a monthly resurgence, as seen in Figure 2. Why it continues to gain strength with each monthly appearance remains unknown.6
We call this model the Random Constant Spread (RCS) model. The model assumes
that the worm had a good random number generator that is properly seeded. We
define 
as the total number of vulnerable servers which can be
potentially compromised from the Internet. (We make the approximation that is fixed--ignoring both patching of systems during the
worm spread and normal deploying and removing of systems or turning on and off
of systems at night. We also ignore any spread of the worm behind firewalls on
private Intranets).
is the initial compromise rate. That is, the number of
vulnerable hosts which an infected host can find and compromise per hour at the
start of the incident, when few other hosts are compromised. We assume that is a global constant, and does not depend on the
processor speed, network connection, or location of the infected machine.
(Clearly, constant is only an approximation.) We assume that a compromised
machine picks other machines to attack completely at random, and that once a
machine is compromised, it cannot be compromised again, or that if it is, that
does not increase the rate at which it can find and attack new systems. We
assume that once it is compromised, it stays that way.
is a time which fixes when the incident happens.
We then have the following variables:
is the proportion of vulnerable machines which have
been compromised.
is the time (in hours). Now, we analyze the problem by assuming that at some particular time , a proportion of the machines have been compromised, and then asking how many more
machines, 
, will get compromised in the next amount of time 
. The answer is:
 |
(1) |
) times the number of machines each compromised machine
can compromise per unit time (
), times the increment of time (). (Note that machines can compromise others per unit time to begin with, but only 
once a proportion of other machines are compromised
already.)
This give us the differential equation:
 |
(2) |
 |
(3) |
where is a constant of integration that fixes the time position
of the incident. This equation has been well known for many years as the
logistic equation, and governs the rate of growth of epidemics in finite
systems when all entities are equally likely to infect any other entity (which
is true for randomized spreading among Internet-connected servers, in the
absence of firewall filtering rules that differentially affect infectability
from or to different addresses).
This is an interesting equation. For early (significantly before ), grows exponentially. For large (significantly after ), goes to 
(all vulnerable machines are compromised). The rate at
which this happens depends only on (the rate at which one machine can compromise others),
and not at all on the number of machines. This is interesting because it tells
us that a worm like this can compromise all vulnerable machines on the Internet
fairly fast.
-axis is the hour of the day (CDT time zone), while the
-axis is probe rate, the number of different
IP addresses seen, and a fit to the data discussed in the
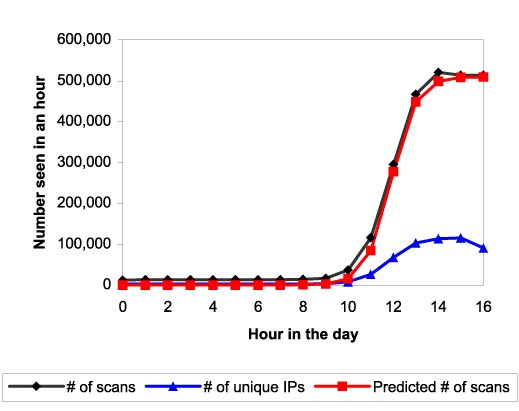
text.Figure 3
shows hourly probe rate data from Ken Eichmann of the Chemical Abstracts Service
for the hourly probe rate inbound on port 80 at that site. Also shown is a fit
to the data with 
, 
, and with the top of the fit scaled to a maximum probe
rate of 510,000 scans/hour. (We fit it to fall slightly below the data
curve, since it seems there is a fixed background rate of web probes that was
going on before the rapid rise due to the worm spread.) This very simple theory
can be seen to give a reasonable first approximation explanation of the worm
behavior. See also Section 4.3
for validation of the theory via simulation.
Note that we fit the scan rate, rather than the number of distinct IPs seen at this site. The incoming scan rate seen at a site is directly proportional to the total number of infected IPs on the Internet, since there is a fixed probability for any worm copy to scan this particular site in the current time interval. However, the number of distinct IPs seen at a site is distorted relative to the overall infection curve. This is because a given worm copy, once it is infected, will take some amount of time before it gets around to scanning any particular site. For a small address space, this delay can be sizeable and causes the distinct IP graph at the given site to lag behind the overall Internet infection rate graph.
Two implications of this graph are interesting. One is that the worm came
close to saturating before it turned itself off at midnight UTC (1900 CDT),
as the number of copies ceased increasing a few hours before the worm's
automatic turnoff. Thus it had found the bulk of the servers it was going to
find at this time. Secondly, the infection rate was about 
per hour--in the early stages of the infection,
each infected server was able to find about other servers per hour.
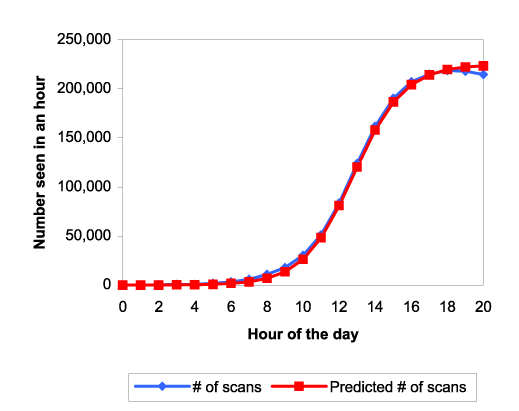
Although Code Red I turned itself off at midnight UTC on July 19th,
hosts with inaccurate clocks kept it alive and allowed it to spread again when
the worm code allowed it to re-awaken on August 1st. Figure 4
shows similar data and fit for that incident. The here is about 
. Since the worm code-base was the same, this lower spread
rate indicates that the number of vulnerable systems was a little less than 40%
as many as the first time around. That is, the data appears consistent with
slightly more than half the systems having been fixed in the 
days intervening.
In this section, we explore the strategies adopted by the two major worms released subsequent to Code Red I: "Code Red II" and "Nimda."
The Code Red II worm was released on Saturday August 4th, 2001 and spread rapidly [CE01,SA01]. The worm code contained a comment stating that it was "Code Red II," but it was an unrelated code base. It did use the same vulnerability, however--a buffer overflow in Microsoft's IIS Web server with CVE number CVE-2001-0500. When successful, the payload installed a root backdoor allowing unrestricted remote access to the infected host. The worm exploit only worked correctly when IIS was running on Microsoft Windows 2000; on Windows NT it caused a system crash rather than an infection.
The worm was also a single-stage scanning worm that chose random IP addresses
and attempted to infect them. However, it used a localized scanning strategy,
where it was differentially likely to attempt to infect addresses close to it.
Specifically, with probability 
it chose a random IP address from within the class B
address space (/16 network) of the infected machine. With probability 
it chose randomly from its own class A (/8 network).
Finally, with probability 
it would choose a random address from the whole Internet.
This strategy appears quite successful. The localized spreading allows the worm to quickly infect parts of the Internet that contain many vulnerable hosts, and also means that the infection often proceeds quicker since hosts with similar IP addresses are often close together in the network topology also. This strategy also allows a worm to spread very rapidly within an internal network once it manages to pass through the external firewall.
Unfortunately, developing an analytic model for the spread of a worm employing this type of localized scanning strategy is significantly more difficult than the modeling effort in Section 2, because it requires incorporating potentially highly non-homogeneous patterns of population locality. The empirical data is also harder to interpret, because Code Red I was quite active when Code Red II was released. Indeed, it appears that Code Red II took a while to overcome Code Red I (see Figure 1), but fully determining the interplay between the two appears to be a significant undertaking.
As well illustrated by the Nimda worm/virus (and, indeed, the original Internet Worm [Sp89,ER89]), malevolent code is not restricted to a single technique. Nimda began on September 18th, 2001, spread very rapidly, and maintained itself on the Internet for months after it started. Nimda spread extensively behind firewalls, and illustrates the ferocity and wide reach that a multi-mode worm can exhibit. The worm is thought to have used at least five different methods to spread itself.
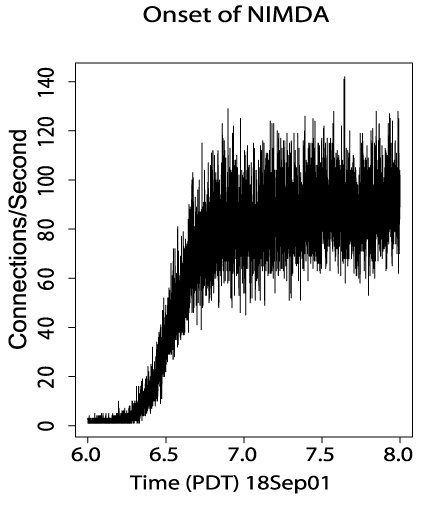
Figure 5
illustrates how rapidly the worm tried to infect one site, the Lawrence Berkeley
National Laboratory. The -axis plots hours past midnight, PDT, while the -axis plots HTTP connection attempts per second. Only
connections from hosts confirmed to have harbored Nimda are counted, to avoid
possible confusion with concurrent Code Red connection attempts. After the onset
of the infection, the total rate of probing was about 3 times that from the
hosts subsequently confirmed to harbor Nimda.
Clearly, onset was quite rapid, rising in just half an hour from essentially no probing to a sustained rate of nearly 100 probes/sec.
There is an additional synergy in Nimda's use of multiple infection vectors: many firewalls allow mail to pass untouched, relying on the mail servers to remove pathogens. Yet since many mail servers remove pathogens based on signatures, they aren't effective during the first few minutes to hours of an outbreak, giving Nimda a reasonably effective means of crossing firewalls to invade internal networks.
Finally, we note that Nimda's full functionality is still not known: all that is known is how it spreads, but not what it might be capable of doing in addition to spreading, if it receives the right trigger, or a prearranged time rolls around. We return to this point in Section 7.
There are several techniques which, although not yet employed, could further significantly increase the virulence of a worm. Beyond the obvious factors of discovering more widespread security holes and increasing the scanning rate, some additional strategies a worm author could employ are: (i) hit-list scanning, (ii) permutation scanning, (iii) topologically aware worms, and (iv) Internet scale hit-lists. The goal is very rapid infection--in particular, considerably faster than any possible human-mediated response.
A worm's scanner can obviously be made significantly faster than the ones
seen today, by careful use of threading and an understanding of the protocols.
By having many requests outstanding, a worm should be capable of scanning
targets at a rate proportional to its access bandwidth. Since it only takes
40 bytes for a TCP SYN packet to determine if a service is accessible,
and often only a few hundred bytes to attempt an exploit, the potential scans
per second can easily exceed 100 for even poor Internet connections. This
increases by allowing a worm to search for a greater number of
targets in a given period of time.
Similarly, the more widespread the vulnerable software is, the faster a worm
using that vulnerability can spread, because each random scan of the network is
more likely to pick up a target, also increasing . We should therefore expect that worm authors will devote
considerable scrutiny to highly homogeneous, highly deployed services, both for
the faster spreading and for the greater number of machines that could be
compromised in a single attack.
One of the biggest problems a worm faces in achieving a very rapid rate of infection is "getting off the ground." Although a worm spreads exponentially during the early stages of infection, the time needed to infect say the first 10,000 hosts dominates the infection time, as can be seen in Figure 3.
There is a simple way for an active worm to overcome this obstacle, which we term hit-list scanning. Before the worm is released, the worm author collects a list of say 10,000 to 50,000 potentially vulnerable machines, ideally ones with good network connections. The worm, when released onto an initial machine on this hit-list, begins scanning down the list. When it infects a machine, it divides the hit-list in half, communicating half to the recipient worm, keeping the other half.
This quick division ensures that even if only 10-20% of the machines on the hit-list are actually vulnerable, an active worm will quickly go through the hit-list and establish itself on all vulnerable machines in only a few seconds. Although the hit-list may start at 200 kilobytes, it quickly shrinks to nothing during the partitioning. This provides a great benefit in constructing a fast worm by speeding the initial infection.
The hit-list needn't be perfect: a simple list of machines running a particular server type may suffice, although greater accuracy will improve the spread. The hit-list itself can be generated using one or several of the following techniques, prepared well in advance, generally with little fear of detection.
Indeed, some individuals produced active countermeasures to Code Red II by exploiting this observation, when combined with the backdoor which Code Red II installs [DA01]. However, it is not a given that future worms will broadcast their presence, and we also note that worms could readily fix the very security holes they exploit (such as is often already observed for attackers performing break-ins manually), which undermines the superficially appealing countermeasure of using the worm's vector as a means by which to disable it.
Another limitation to very fast infection is the general inefficiency of random scanning: many addresses are probed multiple times. Similarly there is no means for a randomly scanning worm to effectively determine when all vulnerable machines are infected. Permutation scanning solves these problems by assuming that a worm can detect that a particular target is already infected.
In a permutation scan, all worms share a common pseudo random permutation of the IP address space. Such a permutation can be efficiently generated using a 32-bit block cipher and a preselected key: simply encrypt an index to get the corresponding address in the permutation, and decrypt an address to get its index.
Any machines infected during the hit-list phase (or local subnet scanning) start scanning just after their point in the permutation, working their way through the permutation, looking for vulnerable machines. Whenever the worm sees an already infected machine, it chooses a new, random start point and proceeds from there. Worms infected by permutation scanning would start at a random point.
This has the effect of providing a self-coordinated, comprehensive scan while
maintaining the benefits of random probing. Each worm looks like it is
conducting a random scan, but it attempts to minimize duplication of effort. Any
time an instance of the worm, 
, encounters an already-infected host, it knows that 
, the original infector of the host, is already working
along the current sequence in the permutation, and is further ahead. Hence,
there's no need for to continue working on the current sequence in addition
to .
Self-coordination keeps the infection rate high and guarantees an eventual comprehensive scan. Furthermore, it allows the worm to make a local decision that further scanning is of little benefit. After any particular copy of the worm sees several infected machines without discovering new vulnerable targets, the worm assumes that effectively complete infection has occurred and stops the scanning process.
A timer could then induce the worms to wake up, change the permutation key to the next one in a prespecified sequence, and begin scanning through the new permutation, starting at its own index and halting when another instance is discovered. This process insures that every address would be efficiently rescanned at regular intervals, detecting any machines which came onto the net or were reinstalled but not patched, greatly increasing a worm's staying power. Otherwise, the worms are silent and difficult to detect, until they receive attack orders (see Section 6).
A further optimization is a partitioned permutation scan. In this scheme, the worm has a range of the permutation that it is initially responsible for. When it infects another machine, it reduces its range in half, with the newly infected worm taking the other section. When the range gets below a certain level, it switches to simple permutation scanning and otherwise behaves like a permutation scan. This scheme offers a slight but noticeable increase in scanning efficiency, by dividing up the initial workload using an approximate divide-and-conquer technique.
Permutation scanning interacts particularly well with a worm which attacks multiple security holes: after deciding that the initial exploit is exhausted, the worm resets the permutation to its current address, changes the permutation key, and exploits the second security hole. Thus, even relatively rare secondary holes can be efficiently and quickly scanned once the worm has established itself on the network.
It may seem that the permutation scanning algorithm is spoofable, but only to a very limited degree. If an uninfected machine responds to the scan in the same way as a worm, by falsely claiming to be infected, it will temporarily protect those machines which exist later in the current permutation from being scanned by the worm. However, since the permutation itself changes on every rescan, the set of machines protected is constantly changing. The result is that unless a very large number of uninfected machines respond to probes like an actual worm, the protection is almost nonexistent.
A combination of hit-list and permutation scanning can create what we term a Warhol worm, capable of attacking most vulnerable targets in well under an hour, possibly less than 15 minutes. Hit-list scanning greatly improves the initial spread, while permutation scanning keeps the worm's infection rate high for much longer when compared with random scanning.
In order to evaluate the effects of hit-list and permutation scanning, we
wrote a small, abstract simulator of a Warhol worm's spread. The simulator
assumes complete connectivity within a 
entry address space7
using a pseudo-random permutation to map addresses to a subset of vulnerable
machines. We used a 32-bit, 6-round variant of RC5 to generate all permutations
and random numbers.
We can parameterize the simulation in terms of: the number of vulnerable machines in the address space; scans per second; the time to infect a machine; number infected during the hit-list phase; and the type of secondary scan (permutation, partitioned permutation, or random). The simulator assumes multithreaded scanning.
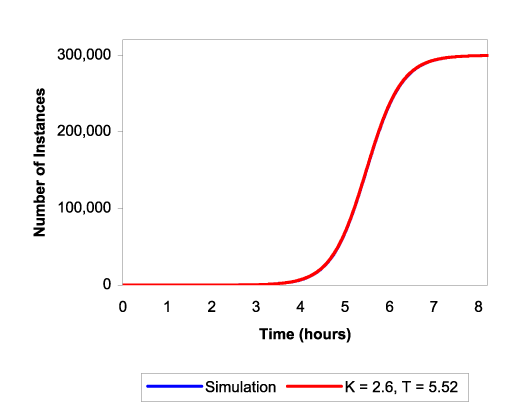
To ensure that the simulator produces reasonable results, Figure 6
shows a comparison between the simulator's output and the model developed in
Section 2,
for a worm capable of 10 scans/second in a population of 300,000 vulnerable
machines. The simulation results fit the model for 
and 
. This represents a worm which is slightly faster (less
than 
) than Code Red I.
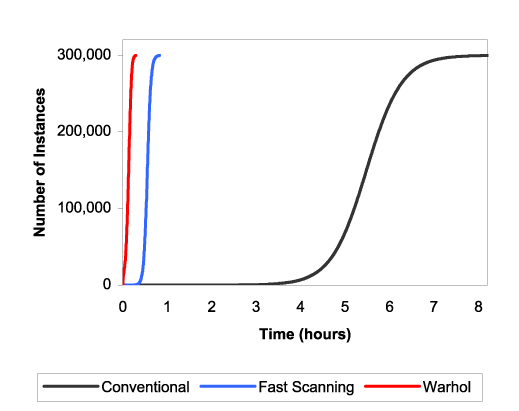
Figure 7 then shows how both faster scanning and the Warhol strategies affect the propagation time. The faster scanning worm (capable of 100 scans/second) reduces the infection time down to under an hour, while the combination of hit-list scanning, permutation scanning, and fast scanning, further reduces infection time to roughly 15 minutes.
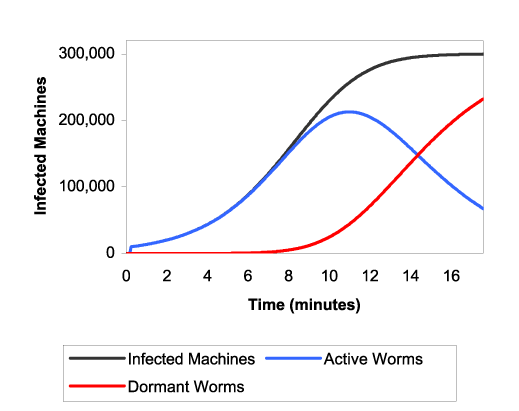
Figure 8 shows in more detail the behavior of the Warhol strategies. It gets a huge boost from the hit-list during the first few seconds of propagation, quickly establishing itself on the network and then spreading exponentially. As the infection exceeds the 50% point, some of the worms begin recognizing that saturation is occurring and stop scanning. By the time the graph ends (at 99.99% of the simulated population), most of the worms have gone silent, leaving a few remaining worms to finish scanning the last of the address space.
An alternative to hit-list scanning is topologically aware scanning, which uses information contained on the victim machine in order to select new targets. Email worms have used this tactic since their inception, as they harvest addresses from their victim in order to find new potential targets, as did the Morris worm (necessary because of the very sparse address space when it was released) [Sp89,ER89].
Many future active worms could easily apply these techniques during the initial spread, before switching to a permutation scan once the known neighbors are exhausted. An active worm that attacked a flaw in a peer-to-peer application could easily get a list of peers from a victim and use those peers as the basis of its attack, which makes such applications highly attractive targets for worm authors. Although we have yet to see such a worm in the wild, these applications must be scrutinized for security. These applications are also vulnerable to contagion worms, as discussed in Section 5.
Similarly, a worm attacking web servers could look for URLs on disk and use these URLs as seed targets as well as simply scanning for random targets. Since these are known to be valid web servers, this would tend to greatly increase the initial spread by preferentially probing for likely targets.
We further observe that there is a variant of the hit-list strategy that could plausibly result in most of the vulnerable servers on the Internet being infected in tens of seconds. We term this a flash worm.
The nub of our observation is that an attacker could plausibly obtain a hit-list of most servers with the relevant service open to the Internet in advance of the release of the worm.8
In addition to the methods already discussed for constructing a hit-list in Section 4.1, a complete scan of the Internet through an OC-12 connection would complete quickly. Given a rate of 750,000 TCP SYN packets per second (the OC-12 provides 622 Mbps, the TCP segment takes 40 bytes, and we allow for link-layer framing), and that the return traffic is smaller in volume than the outbound (it is comprised of either same-sized SYN ACKs or RSTs, smaller ICMPs, or, most often, no response at all), it would take roughly 2 hours to scan the entire address space. Faster links could of course scan even faster. Such a brute-force scan would be easily within the resources of a nation-state bent on cyberwarfare.
Given that an attacker has the determination and foresight to assemble a list
of all or most Internet connected addresses with the relevant service(s) open, a
worm can spread most efficiently by simply attacking addresses on that list. For
example, there are about 
million Web servers on the Internet (according to
Netcraft [Ne02]),
so the size of that particular address list would be 48 MB, uncompressed.
The initial copy of the worm can be programmed to divide the list into 
blocks, and then to find and infect the first address in
each block (or an especially chosen high-bandwidth address in that block), and
then hand the child worm the list of addresses for that block. That copy of the
worm can then re-iterate the process to infect everything in its block. A
threaded worm could begin infecting hosts before it had received the full host
list from its parent to work on, to maximize the parallelization process, and it
could start work on looking for multiple children in parallel.
This design is somewhat fragile if an early copy of the worm is neutralized very quickly, or infects a site from which it cannot scan out. To mitigate this, the worm copies could overlap in their scanning so that all addresses were scanned a small number of times, with every target address being scanned by different paths through the infection tree. This has the additional side-effect of removing the need for further parent-to-child communication after initial infection occurs.
A related design would call for most of the address list to be located in pre-assigned chunks on one or a number of high-bandwidth servers that were well-known to the worm. Each copy of the worm would receive an assignment from its parent, and then fetch the address list from there. The server would only have to send out portions of the list, not the entire list; in principle, it should only have to transmit each address in the list once. In addition, after the worm has propagated sufficiently that a large number of copies are attempting to fetch their (now quite small) lists, at that point the worm collective could switch to sending around the address list with each new infection, rather than having the infectees each contact the server.
This process will result in relatively little wasted effort. For example, if
the worm had a list of Web servers, and a zero-day IIS vulnerability, about 
of the list would be vulnerable. No server would be
probed twice. If 
, then the infection tree for the 
million vulnerable servers would be just 
layers deep.
The spread rate of such a worm would likely be constrained by one of two
things. The worm itself is likely to be small (Code Red I was about
4 KB, and a highly malicious worm could easily be less than 100 KB,
even allowing for a complex payload). Thus, at the start, the address list is
much larger than the worm itself, and the propagation of the worm could be
limited by the time required to transmit the host list out of the initial
infection site or servers where it was stored. Since all the children of the
infection will have much smaller lists to transmit, these later lists are less
likely to limit the worm spread (unless a first generation child has less than
of the initial copy's bandwidth available to it). The
exact time required to transmit the list will depend on the available bandwidth
of the storage sites. As an example, however, we point out that a 48 MB
address list could be pushed down an OC-12 link in less than a second.9
Thus, starting the worm on a high-bandwidth link is desirable for the attacker, and bandwidth is probably a concern at the next layer or two. Compression of the list could make the list delivery much faster. Indeed, we took a sorted list of the 9 million server addresses discussed in Section 5 and found that gzip compression shrinks the list from 36 MB to 13 MB, and differencing the addresses prior to compression reduced it to 7.5 MB.
Another possible limitation is simply the latency required to infect each new
layer in the tree. Given that probes can be issued in parallel, and
substantially more threads can be spawned than (the number of children), we do not have to add up the
time required for a given copy to cycle through its list, but simply take the
maximum infection latency. A single second is a reasonable latency, but with
and a large hit-list to transfer, it might take a little
longer to get 10 copies of the worm through a given site's link. However, not
much longer--if a 5 KB worm can get 50% utilization through a 256 Kbps
DSL uplink, it can transmit ten copies of itself in three seconds. That leads to
a sub-thirty-second limit on the total infection time, given an infection tree
seven layers deep and a design where the new worm children go to a server for
their addresses. (An additional concern here is the possibility of elements of
the worm interfering with one another, either directly, by inducing congestion,
or indirectly, for example by overflowing ARP tables, as happened during the
Code Red I outbreak [SA01].
These possibilities are difficult to analyze.)
In conclusion, we argue that a compact worm that begins with a list including all likely vulnerable addresses, and that has initial knowledge of some vulnerable sites with high-bandwidth links, appears able to infect almost all vulnerable servers on the Internet in less than thirty seconds.
The great speed with which the worms described in the previous sections can propagate presents a grave threat to the Internet's security, because there is so little time available to react to their onset. Still, there might be a possibility of devising mechanisms that automatically detect the spread of such worms and shut them down in some fashion [MSVS02]. Such mechanisms would likely be triggered by the singular communication patterns the worms evince--hosts generating much more diverse and rapid Internet traffic than they usually do.
We now turn to a different paradigm of worm propagation, contagion, which, while likely spreading significantly slower than the rapidly-propagating worms, evinces almost no peculiar communication patterns. As such these worms could prove much more difficult to detect and counter, allowing a patient attacker to slowly but surreptitiously compromise a vast number of systems.
The core idea of the contagion model can be expressed with the following
example. Suppose an attacker has attained a pair of exploits: 
, which subverts a popular type of Web server;
and 
, which subverts a popular type of Web client (browser).
The attacker begins the worm on a convenient server or client (it doesn't matter
which, and they could start with many, if available by some other means), and
then they simply wait. If the starting point is a server, then they wait for
clients to visit (perhaps baiting them by putting up porn content and taking
care that the large search engines index it). As each client visits, the
subverted server detects whether the client is vulnerable to . If so, the server infects it, sending along
both and . As the client's user now surfs other sites, the infected
client inspects whether the servers on those sites are vulnerable to , and, if so, again infects them, sending along and .
In this fashion, the infection spreads from clients to servers and along to other clients, much as a contagious disease spreads based on the incidental traffic patterns of its hosts.
Clearly, with the contagion model there are no unusual communication patterns to observe, other than the larger volume of the connections due to the worm sending along a copy of itself as well as the normal contents of the connection--in the example, the URL request or the corresponding page contents. Depending on the type of data being transferred, this addition might be essentially negligible (for example, for MP3s). Thus, without an analyzer specific to the protocol(s) being exploited, and which knows how to detect abnormal requests and responses, the worm could spread very widely without detection (though perhaps other detection means such as Tripwire file integrity checkers [Tw02] might discover it).
In addition to exploiting the natural communication patterns to spread the worm, these might also be used by the attacker to then control it and retrieve information from the infected hosts, providing that the endemic traffic patterns prove of sufficient frequency and volume for the attacker's purposes. (Or, of course, the attacker might more directly command the infected hosts when the time is ripe, "blowing their cover" in the course of a rapid strike for which keeping the hosts hidden can now be sacrificed.)
As described above, one might find contagion worms a clear theoretical threat, but not necessarily such a grave threat in practice. The example requires a pair of exploits, and will be limited by the size of the populations vulnerable to those attacks and the speed with which Web surfing would serve to interconnect the populations. While some argue the Web exhibits the "small world" phenomenon [Br+00], in which the distance between different Web items in the hypertext topology is quite low, this doesn't necessarily mean that the dynamic patterns by which users visit that content exhibit a similar degree of locality.
We now present a more compelling example of the latent threat posed by the contagion model, namely leveraging peer-to-peer (P2P) systems. P2P systems generally entail a large set of computers all running the same software. Strictly speaking, the computers need only all run the same protocol, but in practice the number of independent implementations is quite limited, and it is plausible that generally a single implementation heavily dominates the population.
Each node in the P2P network is both a client and a server.10Accordingly, the problem of finding a pair of exploits to infect both client and server might likely be reduced to the problem of finding a single exploit, significantly less work for the attacker. P2P systems have several other advantages that make them well suited to contagion worms: (i) they tend to interconnect with many different peers, (ii) they are often used to transfer large files, (iii) the protocols are generally not viewed as mainstream and hence receive less attention in terms of monitoring by intrusion detection systems and analysis of implementation vulnerabilities, (iv) the programs often execute on user's desktops rather than servers, and hence are more likely to have access to sensitive files such as passwords, credit card numbers, address books, and (v) the use of the P2P network often entails the transfer of "grey" content (e.g., pornography, pirated music and videos), arguably making the P2P users less inclined to draw attention to any unusual behavior of the system that they perceive.
The final, sobering quality of P2P networks for forming contagion worms is their potentially immense size. We obtained a trace of TCP port 1214 traffic recorded in November, 2001, at the border of a large university. Port 1214 is used by the KaZaA [Ka01] and Morpheus [Mu01] P2P sharing systems (both11built on the FastTrack P2P framework [Fa01]). As of January, 2002, the KaZaA distributors claim that more than 30,000,000 copies have been downloaded [Ka01]. Since our data does not allow us to readily distinguish between KaZaA and Morpheus traffic, for ease of exposition we will simply refer to all of the traffic as KaZaA.
Our KaZaA trace consists of summaries of TCP connections recorded by a passive network monitor. We have restricted the data to only those connections for which successful SYN and FIN handshakes were both seen (corresponding to connections reliably established and terminated, and eliminating unsuccessful connections such as those due to scanning).
The volume of KaZaA traffic at the university is immense: it comprises 5-10 million established connections per day. What is particularly striking, however, is the diversity of the remote hosts with which hosts at the university participated in KaZaA connections. During the month of November, 9 million distinct remote IP addresses engaged in successful KaZaA connections with university hosts. (There were 5,800 distinct university KaZaA hosts during this time.)
Distinct addresses do not directly equate to distinct computers. A single address can represent multiple computers due to the use of NAT, DHCP, or modem dialups accessed by different users. On the other hand, the same computer can also show up as different addresses due to these mechanisms. Thus, we do not have a precise sense of the number of distinct computers involved in the November trace, but it appears reasonable to estimate it as around 9 million.
KaZaA uses a variant of HTTP for framing its application protocol. Given HTTP's support for variable-sized headers, it would not be surprising to find that a buffer overflow exploit of KaZaA exists. Given such an exploit, it is apparent that if an attacker started out having infected all of the university's KaZaA hosts, then after a month they would have control of about 9 million hosts, assuming that the KaZaA clients are sufficiently homogeneous that a single exploit could infect them all.12
How plausible is it that the attacker could begin with control over all of the university's KaZaA hosts? Quite: while the goal of the contagion worm is to evade detection, the attacker can likely risk a more blatant attack on a single university. If they can find a university lacking in diligent security monitoring (surely there must be a few of these!), they can then compromise a single host at the university, engage in "noisy" brute-force scanning of the internal hosts to find all of the KaZaA clients, and infect them. They then switch into contagion spreading.13
While the above argues that the attacker could gain the 9 million hosts within a month, the actual spread is likely much faster, because once a remote host is infected, it too contributes to spreading the contagion. Not only does this accelerate the epidemic, but it also likely turns it into a pandemic, because the remote hosts can connect with other remote hosts that wouldn't happen to visit the university. Furthermore, depending on the protocol, a single infected node could pretend to have information it doesn't have, in order to appear highly attractive and increase the number of connections received, although that would somewhat disrupt the normal patterns of communication.
We would like therefore to better understand the rate at which a KaZaA contagion worm could spread, and to what breadth. To estimate this from just the university trace is difficult, because we don't know the total size of the KaZaA population. Doubtless it is larger than 9,000,000--but is it as high as 30,000,000, as indicated in [Ka01]? How many of those copies were redundant (same user fetching the software multiple times), or are no longer in use? On the other hand, could the population be higher, due to users getting copies of the clients from other sources than [Ka01]?
Another problem is that we do not know the degree to which the university's hosts are "typical." We also lack any traces of their internal peer-to-peer traffic, which, if frequent, would have major implications for the rate at which the worm could infect an entire remote site.
We are pursuing further work in this area. First, we are attempting with colleagues to develop graph-based models with which we can then extrapolate properties of the spread of the contagion based on different sets of assumptions about the hosts in our trace. Second, we have obtained traces of KaZaA traffic from another university (in another country), and will be analyzing these to determine the degree of overlap and cross-talk between the two universities, with which to then better estimate the total KaZaA population and its communication patterns. Finally, we are building a simulator for both active and contagion worms within various peer-to-peer topologies.
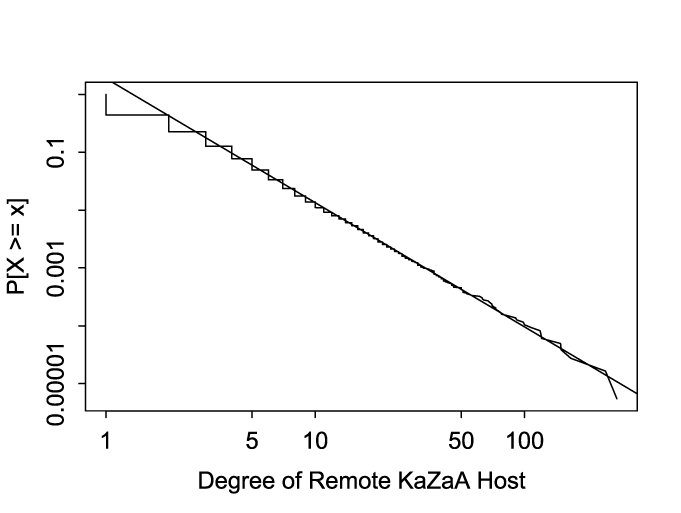
.As a last comment, we have evidence that the KaZaA network may behave
like a "scale-free" topology in terms of its interconnection. Figure 9
shows the distribution of the degree of the remote hosts in the trace, i.e., the
number of distinct local hosts to which each remote host connected during
November, 2001. The plot is shown as a log-log complementary distribution
function: the -axis shows 
of the remote host's degree, and the -axis shows of the probability of observing a remote host with that
outdegree or higher. (Due to the immense size of the dataset, we plot a subset
rather than the entire dataset, randomly sampled with 
.)
A straight line on such a plot corresponds to a Pareto distribution.
While the majority of the remote hosts connected to only one or two local hosts,
for those connecting to three or more hosts, the fit to a Pareto distribution
(with shape parameter ) is compelling. That the degree has such a distribution
is then strongly suggestive that the underlying KaZaA network may exhibit
a scale-free (or Zipf-like) topology. The propagation of contagion through such
networks has recently been studied [PV01].
While the discussion in that article is flawed--it confounds the Internet's
underlying IP topology with email and Web application topology--the general
framework the authors develop gives hope that we can leverage it to better
understand the behavior of a KaZaA contagion worm. That said, we add that
the degree of the local hosts is clearly not Pareto, so the
analysis might not in fact apply.
The last facet of worm design we examine concerns mechanisms by which the attacker can control and modify a worm after its dissemination. The ease and resiliency with which an attacker can do so has serious consequences for both how the threat of a deployed worm can evolve, and the potential difficulty in detecting the worm's presence and operation after the initial infection.
Some previous worms such as the Goner mail worm [CE02] contained primitive remote control code, similar to many common "zombies", allowing the authors and others to issue commands to a distributed DOS module through an IRC [OR93] channel. (Indeed, the root backdoor installed by Code Red II also offered a form of unlimited remote control.) Others worms have attempted to download updates and payloads from web pages, such as W32/sonic [Sy00]. Both of these mechanisms, when employed, were quickly countered by removing the pages and tracking the channels. Similarly, previously seen DDOS tools such as Stacheldraht [Di99] have included both encrypted communication and update mechanisms for directly controlling the zombies.
Here we briefly explore a more sophisticated method--direct worm-to-worm communication and programmable updates--which, while not yet observed in the wild, is a natural evolution based on the previous updatable worms and DDOS tools.
In a distributed-control worm, each worm has a list of other known, running copies of the worm and an ability to create encrypted communication channels to spread information. Any new command issued to the worms has a unique identifier and is cryptographically signed using an author's key. Once a worm has a copy of the command, the command is first verified by examining the cryptographic signature, spread to every other known instance of the worm, and then executed. This allows any command to be initially sent to an arbitrary worm instance, where it is then quickly spread to all running copies.
The key to such a network is the degree of connectivity maintained, in order to overcome infected hosts being removed from the network, and to hasten the spread of new commands. Although it is clear that a worm could spread information to its neighbors about other worm instances in order to create a more connected, highly redundant network, it is useful to estimate the initial degree of connectivity without these additional steps.
If each worm node only knows about other nodes it has probed, infected, or been probed by, the average connectivity is still very high. With 1M hosts, using permutation scanning (with no halting), our simulator shows that the average degree of nodes in the worm network is 4 when 95% infection is achieved, and 5.5 when 99% infection is achieved. Additionally, each permutation-based rescan will add 2 to the degree of every worm, representing the copy discovered by each instance, and the copy which discovers each instance. Thus, after a couple of rescans, the connectivity becomes very high without requiring additional communication between the worm instances.
Such a network could be used to quickly pass updates to all running copies, without having a single point of communication like that seen in previous worms, increasing the staying power by preventing the communication channel from being disrupted or co-opted by others, while still allowing the author to control their creation in a difficult-to-track manner.
The commands to a worm can of course be arbitrary code. Many operating systems already support convenient dynamic code loading, which could be readily employed by a worm's author. Another possibility has the bulk of the worm written in a flexible language combined with a small interpreter. By making the worm's commands be general modules, a huge increase in flexibility would be achieved.
Of particular interest are new attack modules and seeds for new worms. If the author discovers a new security hole and creates a new attack module, this could be released into the worm network. Even if only a few thousand copies of the worm remain, this is enough of an installed base for a hit-list like effect to occur upon introduction of a new attack module, quickly spreading the worm back through the network.
It is an interesting question whether it is possible for a worm author to release such a worm with the cryptographic modules correctly implemented. From experience, if the worm author attempts to build their own cryptographic implementation, this could well suffer from a significant weakness that could be exploited for countering the worm. Yet there are a number of strong cryptographic applications and libraries that could be used by a worm author to provide the cryptographic framework, a good example being OpenSSL [Op01], which includes an encrypted session layer, symmetric ciphers, hash functions, and public key ciphers and signatures to provide for code signing.
Given the magnitude of Internet-scale threats as developed in the previous sections, we believe it is imperative for the Internet in general, and for nations concerned with cyberwarfare in particular, to attempt to counter the immense risk. We argue that use of biological metaphors reflected in the terms "worms" and "viruses" remains apt for envisioning a nation-scale defense: the cyber equivalent of the Centers for Disease Control and Prevention in the United States [CDC02], whose mission is to monitor the national and worldwide progression of various forms of disease, identify incipient threats and new outbreaks, and actively foster research for combating various diseases and other health threats.
We see an analogous "Cyber-Center for Disease Control" (CDC) as having six roles:
As discussed earlier in this paper, to date Internet-scale worms have been identified primarily via informal email discussion on a few key mailing lists. This process takes hours at a minimum, too slow for even the "slower" of the rapidly-propagating worms, much less the very fast worms developed in Section 4. The use of mailing lists for identification also raises the possibility of an attacker targeting the mailing lists for denial-of-service in conjunction with their main attack, which could greatly delay identification and a coordinated response. Present institutions for analyzing malicious code events are not able to produce a meaningful response before a fast active worm reaches saturation.
CDC Task: develop robust communication mechanisms for gathering and coordinating "field information." Such mechanisms would likely be (i) decentralized, and (ii) span multiple communication mechanisms (e.g., Internet, cellular, pager, private line).
For flash worms, and probably Warhol worms, arguably no human-driven communication will suffice for adequate identification of an outbreak before nearly complete infection is achieved.
CDC Task: sponsor research in automated mechanisms for detecting worms based on their traffic patterns; foster the deployment of a widespread set of sensors. The set of sensors must be sufficiently diverse or secret such that an attacker cannot design their worm to avoid them. This requirement may then call for the development of sensors that operate within the Internet backbone, as opposed to at individual sites, and actuators that can respond to various threats (see below).
Clearly, widespread deployment and use of sensors raises potentially immense policy issues concerning privacy and access control. Present institutions lack the authority and mandate to develop and deploy Internet-wide sensors and actuators.
Once a worm pathogen is identified, the next step is to understand (i) how it spreads and (ii) what it does in addition to spreading.
The first of these is likely easier than the second, because the spreading functionality--or at least a subset of it--will have manifested itself during the identification process. While understanding the pathogen's additional functionality is in principle impossible--since it requires solving the Halting Problem--it is important to keep in mind that the Halting Problem applies to analyzing arbitrary programs: on the other hand, there are classes of programs that are fully analyzable, as revealed by extensive past research in proving programmatic correctness.
The question is then to what degree can worm authors write programs that are intractable to analyze. Certainly it is quite possible to take steps to make programs difficult to understand; indeed, there is a yearly contest built around just this theme [NCSB01], and our own unfunded research in this regard has demonstrated to us the relative ease of transforming a non-trivial program into an incomprehensible mess [Pa92].
CDC Task: procure and develop state-of-the-art program analysis tools, to assist an on-call group of experts. These tools would need to go beyond simple disassembly, with facilities for recognizing variants from a library of different algorithms and components from a variety of development toolkits, and also components from previous worms, which would be archived in detail by a CDC staff librarian.
The tools would also need to support rapid, distributed program annotation and simulation. Furthermore, the team would need access to a laboratory stocked with virtual machines capable of running or emulating widely-used operating systems with support for detailed execution monitoring. (Less widely-used systems do not pose much of a threat in regards to Internet-scale worms.) In addition, code coverage analysis tools coupled with sample execution of the pathogen could help identify unexecuted portions of the code, which in turn might reflect the pathogen's additional functionality, and thus merit detailed analysis. (Or such unused regions could simply reflect "chaff" added by the worm author to slow down the analysis; an "arms race" seems inevitable here.)
Admittedly, any analysis involving humans might be too slow to match the pace of a rapidly-propagating worm. But clearly it will always prove beneficial to know exactly how a worm spread and what it did, even after the fact; and for a large-scale cyberwarfare situation, speed will remain of the essence, especially as the "fog of war" may well retard the attacker's full use of the worm. This is especially true if the worm is designed to accept updates, for although the worm's spread may be extremely fast, the threat may continue as long as there are a significant number of infected machines remaining on the Internet. Furthermore, for contagion worms, there may be significantly more time available for analysis, if the worm is detected sufficiently early.
Naturally, we would want the CDC to help as much as possible in retarding the progress or subsequent application of the worm.
CDC Task: establish mechanisms with which to propagate signatures describing how worms and their traffic can be detected and terminated or isolated, and deploy an accompanying body of agents that can then apply the mechanisms.14
It is difficult to see how such a set of agents can be effective without either extremely broad deployment, or pervasive backbone deployment. Both approaches carry with them major research challenges in terms of coordination, authentication, and resilience in the presence of targeted attack. As with sensors, the policy issues regarding the actual deployment of such agents are daunting--who controls the agents, who is required to host them, who is liable for collateral damage the agents induce, who maintains the agents and ensures their security and integrity?
We would want the CDC to not only be reactive, but also proactive: to identify incipient threats.
CDC Task: track the use of different applications in the Internet, to detect when previously unknown ones begin to appear in widespread use. Unfortunately, Internet applications sometimes can "explode" onto the scene, very rapidly growing from no use to comprising major traffic contributors [Pa94]. Accordingly, tracking their onset is not a simple matter, but will require diligent analysis of network traffic statistics from a variety of sources, as well as monitoring fora in which various new applications are discussed (since some of them may have traffic patterns that are difficult to discern using conventional traffic monitoring variables such as TCP/UDP port numbers).
CDC Task: analyze the threat potential of new applications. How widely spread might their use become? How homogeneous are the clients and servers? What are likely exploit strategies for subverting the implementations? What are the application's native communication patterns?
Once a new potential disease vector has been identified, we would then want to deploy analyzers that understand how the protocol functions, to have some hope of detecting contagion worms as they propagate.
For example, to our knowledge there is no KaZaA module (one specific to how KaZaA functions) available for network intrusion detection systems in use today. Without such a module, it would be exceedingly difficult to detect when KaZaA is being exploited to propagate a contagion worm.
CDC Task: foster the development of application analysis modules suitable for integration with the intrusion detection systems in use by the CDC's outbreak-identification elements.
Devising the means to live with an Internet periodically ravaged by flash or contagion worms is at best an uneasy equilibrium. The longer-term requirement is to shift the makeup of Internet applications such that they become much less amenable to abuse. For example, this may entail broader notions of sandboxing, type safety, and inherent limitations on the rate of creating connections and the volume of traffic transmitted over them.
CDC Task: foster research into resilient application design paradigms and infrastructure modifications that (somehow) remain viable for adaptation by the commercial software industry, perhaps assisted by legislation or government policy.
CDC Task: vet applications as conforming to a certain standard of resilience to exploitation, particularly self-propagating forms of exploitation.
A final basic issue regarding the CDC is to what degree should it operate in an open fashion. For example, during an outbreak the CDC could maintain a web site for use by the research community. Such an approach would allow many different people to contribute to the analysis of the outbreak and of the pathogen, perhaps adding invaluable insight and empirical data. This sort of coordination happens informally today, in part; but it is also the case that currently a variety of anti-viral and security companies analyze outbreaks independently, essentially competing to come out with a complete analysis first. This makes for potentially very inefficient use of a scarce resource, namely the highly specialized skill of analyzing pathogens.
A key question then is the cost of operating in an open fashion. First, doing so brings with it its own set of security issues, regarding authenticating purported information uploaded into the analysis database, and preventing an attacker from crippling the analysis effort by launching a side-attack targeting the system. Second, the attacker could monitor the progress made in understanding the worm, and perhaps gain insight into how it has spread beyond what they could directly gather for themselves, allowing them to better hone their attack. Third, some sources of potentially highly valuable empirical data might refuse to make their data available if doing so is to release it to the public at large.
Given these concerns, it seems likely that the CDC would pursue a "partially open" approach, in which subsets of information are made publicly available, and publicly-attained information is integrated into the CDC's internal analysis, but the information flow is scrutinized in both directions. Unfortunately, such scrutiny would surely involve manual assessment, and could greatly slow the collection of vital information.
A related question is how international in scope such a facility should be. A national facility is likely to have a simpler mission and clearer management and accountability. However, there are real benefits to an international approach to this problem; one's allies are awake and working while one sleeps. A worm released in the middle of the night in the US would be far more likely to receive intense early research and attention in Europe or Asia than in the US itself. Thus, at a minimum, national level CDCs are likely to need to maintain strong linkages with one another.
In this paper we have examined the spread of several recent worms that infected hundreds of thousands of hosts within hours. We showed that some of these worms remain endemic on the Internet. We explained that better-engineered worms could spread in minutes or even tens of seconds rather than hours, and could be controlled, modified, and maintained indefinitely, posing an ongoing threat of use in attack on a variety of sites and infrastructures. Thus, worms represent an extremely serious threat to the safety of the Internet. We finished with a discussion of the urgent need for stronger societal institutions and technical measures to control worms, and sketched what these might look like.
Many thanks to Jim Ausman, Michael Constant, Ken Eichmann, Anja Feldmann, Gary Grim, Mark Handley, Roelof Jonkman, Dick Karp, Jon Kuroda, Cathy McCollum, Mike Skroch, Robin Sommer, Laura Tinnel, Dan Upper, David Wagner, and Brian Witten for very helpful discussions, analysis, and measurement data.
This document was generated using the LaTeX2HTML translator Version 2K.1beta (1.50)
Copyright © 1993, 1994, 1995, 1996, Nikos Drakos, Computer
Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999, Ross Moore, Mathematics Department,
Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0
cdc.tex
The translation was initiated by Nicholas C. Weaver on 2002-05-14 and then
hacked up a tad by Vern Paxson on 2002-05-21.